The potentiation is the mathematical operation that represents the multiplication of the same factors. That is, we use the potentiation when a number is multiplied by itself several times.
Take advantage of the commented exercises, proposals and contest questions to test your knowledge about enhancement.
Question 1
Determine the value of each of the powers below.
a) 25 1
b) 150 0
c) (7/9) -2
Answer:
Correct answer: a) 25, b) 1 and c) 81/49.
a) When a power is raised to exponent 1, the result is the base itself. Therefore, 25 1 = 25.
b) When a power is raised to the exponent 0, the result is the number 1. Therefore, 150 0 = 1.
c) In this case, we have a fraction raised to a negative exponent. To solve it, we must invert the base and change the exponent sign.
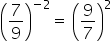
Now, we can raise the numerator and denominator to exponent 2.
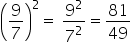
Question 2
Knowing that the value of 5 7 is 78 125, what is the result of 5 8 ?
a) 156 250
b) 390 625
c) 234 375
d) 312 500
Answer:
Correct answer: b) 390 625.
To solve this question we can transform 5 8 into a multiplication of powers of equal bases, since x . a y = a x + y
As we know the value of 5 7 , we transform the number 5 8 as follows:
5 8 = 5 7 . 5, because 5 7 . 5 = 5 7 + 1 = 5 8
So, to find the result, we just need to replace the value of 5 7 and multiply by 5.
5 7 . 5 = 78 125. 5 = 390 625
Question 3
Are the powers (-2) 4 and -2 4 the same or different? And what is the result?
Answer:
Correct answer: The powers are different and have 16 and -16 results, respectively.
When the base of a power is a negative number and is raised to an even exponent, the result will be positive. However, to signal that the base is negative, its value must be in parentheses.
(- 2) 4 = (- 2) x (- 2) x (- 2) x (- 2) = +16
When there are no parentheses separating the base, the negative sign must be included in the result.
– 2 4 = – 16
Therefore, the results are: (- 2) 4 = 16 and – 2 4 = – 16.
Question 4
On one site there are 12 trees. Each tree has 12 branches and each branch has 12 apples. How many apples are there on the farm?
a) 144
b) 1224
c) 1564
d) 1728
Answer:
Correct answer: 1,728 apples.
We have a power where number 12 is the base and number 3 is the number of times the base is repeated.
Let’s take one of the trees as an example. In each of the 12 branches of a tree there are 12 apples, that is, 12 branches times 12 apples: 12 x 12 = 144.
Only in total we have 12 trees, that is, 144 x 12 gives us the total number of apples. This can be expressed in the form of power.
12 x 12 x 12 = 12 3 = 1 728.
Therefore, the site has 1,728 apples.
Question 5
The value of the expression 20x 3 + 2x 2 y 5 , for x = – 4 and y = 2 is :
a) 256
b) – 400
c) 400
d) – 256
Answer
Correct answer: d) – 256.
To solve the expression the first step is to replace the letters with the values, so the expression will be:
20. (- 4) 3 + 2. (- 4) 2 . 2 5
We must be careful with the signals when resolving the potentiation. When the base is negative, the result will be positive if the exponent is even and will be negative when the exponent is odd. Thus, the expression will be:
20. (- 64) + 2. (+16). 32
Now that we have solved the potentiations, let’s solve the other operations, remembering that we first solve the multiplications and then the subtraction.
– 1280 + 1024 = – 256
So, the correct answer is alternative d .
Question 6
(3 6. 3 -2 ): 3 4 is equal to :
a) 0
b) 1
c) 3 -3
d) 3 -8
Correct answer: b) 1.
We can solve the proposed numerical expression in two ways. One is to solve each of the powers first and then solve the other operations. The other way is to use the property of multiplication and division of powers of the same base. We will resolve these two paths.
1st way: Let’s solve the value of each power:
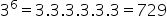
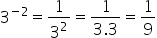
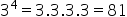
Now we are going to replace the values found in the expression and solve the indicated operations. Remembering that we must first resolve the operation within the parentheses.
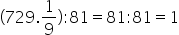
So, the right answer is the letter b.
2nd way : By applying the property, we must remember that in the multiplication of powers of the same base, the base is repeated and the exponents are added. In the division, the base is repeated and the exponents are subtracted. Thus, we have:
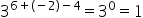
Remembering that every number raised to zero is equal to 1, we arrive at the same result found previously.
Note that in the 2nd form we find the result more easily. Therefore, it is very important to know the boosting properties.
Question 7
Simplifying the expression below, we find :
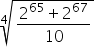
a) 2
b) 2 10
c) 2 15
d) 2 16
Answer:
Correct answer: d) 2 16 .
We must note that the operation between the base 2 powers is the sum. Therefore, we will have to find a way to simplify, because even if we have the same bases we cannot add.
One way to simplify is to try to keep the same exponent in both powers, so we can put it in evidence. For that, let’s write 2 67 as 2 65 . 2 2 , replacing in the expression we have:
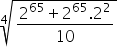
We can highlight the 2 65 as follows:
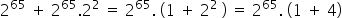
This can be done, since 2 65 multiplying the terms 1 and 4 results in the initial expression.
Simplifying the common terms, we have:
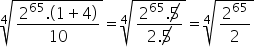
Now we can apply the property of the power division of the same base, remembering that when the exponent does not appear, its value is equal to 1.
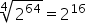
So the answer will be the letter d.
Question 8
Calculate the value of the expression below:
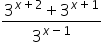
Correct answer: 36.
To resolve this issue, we must first rewrite the terms.
When multiplying powers of the same base, we can repeat the base and add the exponents.
3 x .3 2 = 3 x + 2
3 x .3 = 3 x + 1
In the division of powers of the same base we can repeat the base and subtract the exponents.
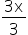
Substituting the values in the expression, we have:
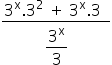
Note that in the numerator the term 3x is repeated and, therefore, we can put it in evidence.
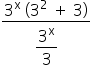
Since we have a division with a fraction, we repeat the numerator of the first and multiply by the inverse of the second to then solve the expression.
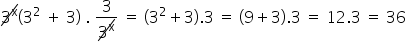
Therefore, the expression’s value is 36.
Question 9
Check whether the sentences are false or true:
a) (x. y) 4 = x 4 . y 4
b) (x + y) 4 = x 4 + y 4
c) (x – y) 4 = x 4 – y 4
d) (x + y) 0 = 1
Answer:
the truth. In this power, whose base is a multiplication, the factors can be raised separately to the exponent before being multiplied.
b) False. The expression is a newton binomial of type (a + b) n . In this case, we have a binomial of degree 4, the result of which is:
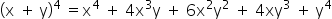
c) False. The expression is a Newton binomial of type (a – b) n . The correct answer is a polynomial:
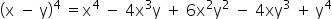
d) True. It is a power with exponent 0 and, therefore, its result must be 1.
Question 10
The value of (0.3) -1 + (- 27) 0.333 … is:
Answer:
Correct answer: 1/3.
To resolve the issue, we must first rewrite the numbers 0.3 and 0.333 … as fractions.
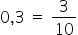
Note that in this case, we just write the number in the numerator and to the denominator we add the number of zeros that corresponds to the number of decimal places after the comma, which is just one.
0.333 … is a periodic tithe and we need to find its generating fraction.
For this, we write the number that is repeated in the periodic tithe in the numerator and divide by 9.
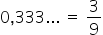
Now, we can replace the values in the expression.
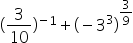
The first term of the expression has a negative exponent. To make it positive, we must invert the power base.
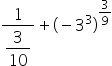
The second term presents a fraction as an exponent. We can then turn it into a root.
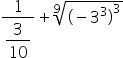
The fractional division is solved by repeating the numerator and multiplying by the inverse of the second.
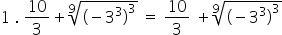
Inside the root we have the power of a power. To solve it, we must maintain the base and multiply the exponents.
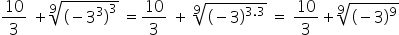
Since the exponent inside the root has the same value as the radical index, we can eliminate the root and solve the expression.
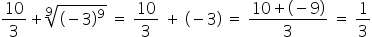
Question 11
(UFRGS – 2015) The digits of the 9 99 – 4 44 units are:
a) 1
b) 2
c) 3
d) 4
e) 5
Answer
Correct alternative: c) 3.
Observe the results below when we raise the bases of expression from the first to the fifth power.
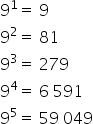
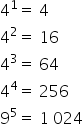
Note that there is the following pattern:
The number 9 when raised to an odd exponent shows the number 9 in the unit box and when raised to an even exponent it shows the number 1 in the unit box.
The number 4 when raised to an odd exponent shows the number 4 in the unit house and when raised to an even exponent it shows the number 6 in the unit house.
Therefore, in the number of the units when performing the expression 9 99 – 4 44 we will find the number 3, since 9 – 6 = 3.
Question 12
(UFRGS – 2013) A healthy human adult is home to about 100 billion bacteria, only in his digestive tract. This number of bacteria can be written as
a) 10 9
b) 10 10
c) 10 11
d) 10 12
e) 10 13
Answer:
Correct alternative: c) 10 11
A billion is the same as a billion, that is, 1000 x 1,000,000 = 1,000,000,000.
100 billion is equal to 100 x 1,000,000,000 = 100,000,000,000.
Large numbers like the one in this question can be written in scientific notation, whose writing follows the N pattern. 10 n , where N is a number less than 10 and greater than or equal to 1. The base 10 exponent is the number of decimal places that the comma “walked” to obtain the value of N.
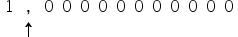
Note that to get to number 11 it was necessary to “walk” 11 decimal places. Therefore, we have the power 10 11 as a result.
Question 13
(Enem – 2012) The North American Space Agency (NASA) reported that the asteroid YU 55 crossed the space between the Earth and the Moon in November 2011. The following illustration suggests that the asteroid traveled its path on the same plane as contains the orbit described by the Moon around the Earth. The figure shows the proximity of the asteroid to Earth, that is, the shortest distance it passed from the Earth’s surface.
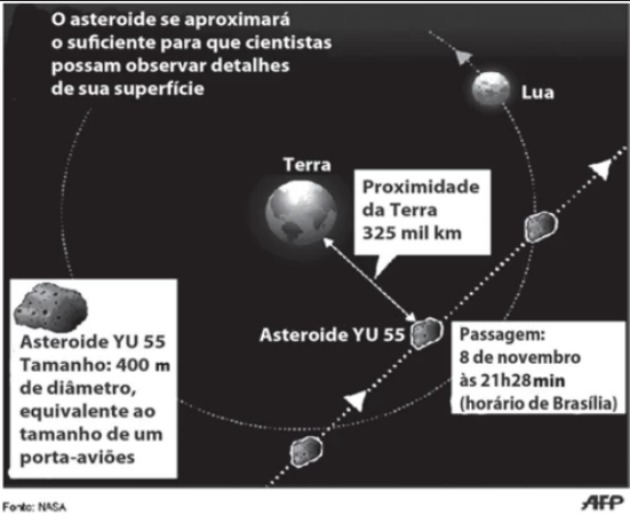
Based on this information, the shortest distance that the asteroid YU 55 passed from the Earth’s surface is equal to
a) 3.25 .10 2 km
b) 3.25 .10 3 km
c) 3.25. 10 4 km
d) 3.25. 10 5 km
e) 3.25. 10 6 km
Answer:
Correct alternative: d) 3.25. 10 5 km
In the figure, it is indicated the shortest distance he passed from the Earth’s surface, which is 325 thousand km, that is, 325 000 km.
This number must be written in scientific notation. For this, we must “walk” with the comma until we find a number less than 10 and greater than or equal to 1. The number of decimal places that the comma “walked” corresponds to the base 10 exponent in the formula N. 10 n .
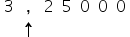
We reached number 3.25 and, for that, the comma “walked” 5 decimal places. Therefore, in scientific notation, the asteroid’s proximity to Earth is 3.25. 10 5 km.
Question 14
(EPCAR – 2011) Simplifying the expression
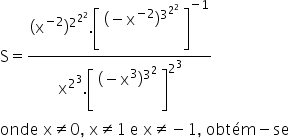
a) – x -94
b) x 94
c) x -94
d) – x 94
Answer
Correct alternative: a) -x -94
First, we rewrite the exponents that are in the form of power.
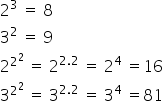
Substituting the values in the expression, we have:
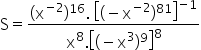
As we have high powers to other exponents, we must conserve the base and multiply the exponents.
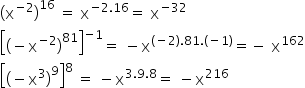
We can then insert the calculated values into the expression.
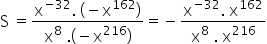
Both in the numerator and in the denominator there is a multiplication of powers of equal bases. To solve them we must repeat the base and add the exponents.
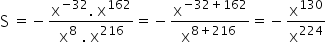
Now, as we owe the division of powers of the same base, we can repeat the base and subtract the exponents.
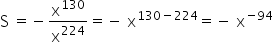
Therefore, the correct alternative is the letter a, the result of which is -x -94 .
Question 15
(Enem – 2016) To celebrate the anniversary of a city, the city organizes four consecutive days of cultural attractions. The experience of previous years shows that, from one day to the next, the number of visitors to the event is tripled. 345 visitors are expected to attend the first day of the event.
A possible representation of the expected number of participants for the last day is
a) 3 × 345
b) (3 + 3 + 3) × 345
c) 3 3 × 345
d) 3 × 4 × 345
e) 3 4 × 345
Answer:
Correct alternative: c) 3 3 × 345
At this point we have a case in geometric progression, for a number multiplied by a ratio (q) correspond to the next set of sequence numbers as the formula
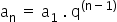
Where:
a n : last day of the event, that is, day 4.
a 1 : number of participants on the first day of the event, which is 345.
q (n-1) : reason, whose exponent is formed by the number we want to obtain minus 1
According to previous experiences, from one day to the next, the number of visitors to the event is tripled, that is, q = 3.
Substituting the values in the formula for the general term, we have:
Therefore, 9 315 people are expected for the last day of the event and a possible representation of the expected number of participants for the last day is 3 3 × 345.
