The area of the sphere corresponds to the measurement of the surface of this spatial geometrical figure. Remember that the sphere is a solid and symmetrical three-dimensional figure.
Formula: How to Calculate?
To calculate the spherical surface area, use the formula:
A e = 4. π .r 2
Where:
A e : sphere area
π (Pi): constant value 3.14
r : radius
Note : the radius of the sphere corresponds to the distance between the center of the figure and its end.
Solved Exercises
Calculate the area of spherical surfaces:
a) sphere of radius 7 cm
A e = 4.π.r 2
A e = 4.π.7
A e = 4.π.49
A e = 196π cm 2
b) 12 cm diameter sphere
First of all, we must remember that the diameter is twice the radius measurement (d = 2r). Therefore, the radius of this sphere measures 6 cm.
A e = 4.π.r 2
A e = 4.π.6 2
A e = 4.π.36
A e = 144π cm 2
c) sphere of volume 288π cm 3
To perform this exercise we must remember the formula for the volume of the sphere:
V and = 4 π .r 3 /3
288 π cm 3 = 4 π .r 3 /3 (cuts the two sides of π)
288. 3 = 4.r 3
864 = 4.r 3
864/4 = r 3
216 = r 3
r = 3 √216
r = 6 cm
Discovered the radius measure, let’s calculate the spherical surface area:
A e = 4.π.r 2
A e = 4.π.6 2
A e = 4.π.36
A e = 144 π cm 2
Vestibular Exercises with Feedback
1 . (UNITAU) By increasing the radius of a sphere by 10%, its surface will increase:
a) 21%.
b) 11%.
c) 31%.
d) 24%.
e) 30%.
Answer
Alternative to: 21%
2 . (UFRS) A sphere of radius 2 cm is immersed in a cylindrical cup of 4 cm radius, until it touches the bottom, so that the water in the glass exactly covers the sphere.
Before the sphere was placed in the glass, the height of water was:
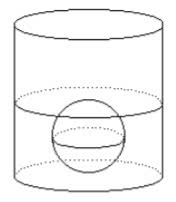
a) 27/8 cm
b) 19/6 cm
c
) 18/5 cm d) 10/3 cm
e) 7/2 cm
Answer
Alternative d: 10/3 cm
3 . (UFSM) The surface area of a sphere and the total area of a straight circular cone are the same. If the radius of the base of the cone measures 4 cm and the volume of the cone is 16π cm 3 the radius of the sphere is given by:
a) √3 cm
b) 2 cm
c) 3 cm
d) 4 cm
e) 4 + √2 cm
Answer
Alternative c: 3 cm