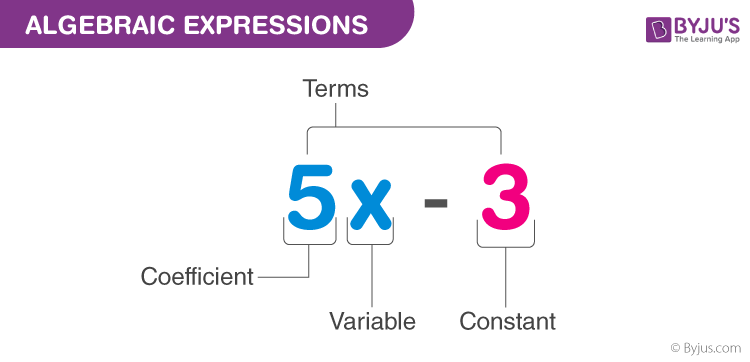
Algebraic expressions are mathematical expressions that present numbers, letters and operations.
Such expressions are often used in formulas and equations.
The letters that appear in an algebraic expression are called variables and represent an unknown value.
The numbers written in front of the letters are called coefficients and should be multiplied by the values assigned to the letters.
Examples
a) x + 5
b) b 2 – 4ac
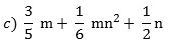
Calculating an Algebraic Expression
The value of an algebraic expression depends on the value that will be assigned to the letters.
To calculate the value of an algebraic expression, we must replace the letter values and perform the indicated operations. Remembering that between the coefficient and the letters, the operation is multiplication.
Example
The perimeter of a rectangle is calculated using the formula:
P = 2b + 2h
Replacing the letters with the indicated values, find the perimeter of the following rectangles

Simplification of Algebraic Expressions
We can write algebraic expressions more simply by adding their similar terms (same literal part).
To simplify, we will add or subtract the coefficients from similar terms and repeat the literal part.
Examples
a) 3xy + 7xy 4 – 6x 3 y + 2xy – 10xy 4 = (3xy + 2xy) + (7xy 4 – 10xy 4 ) – 6x 3 y = 5xy – 3xy 4 – 6x 3 y
b) ab – 3cd + 2ab – ab + 3cd + 5ab = (ab + 2ab – ab + 5ab) + (- 3cd + 3cd) = 7ab
Factoring Algebraic Expressions
Factoring means writing an expression as a product of terms.
Transforming an algebraic expression into a multiplication of terms often allows us to simplify the expression.
To factor an algebraic expression we can use the following cases:
Common factor in evidence : ax + bx = x. (a + b)
Grouping: ax + bx + ay + by = x. (a + b) + y. (a + b) = (x + y). (a + b)
Perfect Square Trinomial (Addition): a 2 + 2ab + b 2 = (a + b) 2
Perfect Square Trinomial (Difference): a 2 – 2ab + b 2 = (a – b) 2
Difference of two squares: (a + b). (a – b) = a 2 – b 2
Perfect Cube (Sum): a 3 + 3a 2 b + 3ab 2 + b 3 = (a + b) 3
Perfect Cube (Difference): a 3 – 3a 2 b + 3ab 2 – b 3 = (a – b) 3
Monomials
When an algebraic expression has only multiplications between the coefficient and the letters (literal part), it is called a monomial.
Examples
a) 3ab
b) 10xy 2 z 3
c) bh (when no number appears in the coefficient, its value is equal to 1)
Similar monomials are those with the same literal part (same letters with the same exponents).
The 4xy and 30xy monomials are similar. The 4xy and 30x 2 y 3 monomials are not similar, since the corresponding letters do not have the same exponent.
Polynomials
When an algebraic expression has sums and subtractions of unlike monomials it is called a polynomial.
Examples
a) 2xy + 3 x 2 y – xy 3
b) a + b
c) 3abc + ab + ac + 5 bc
Algebraic Operations
Addition and subtraction
The algebraic sum or subtraction is done by adding or subtracting the coefficients of similar terms and repeating the literal part.
Example
a) Add (2x 2 + 3xy + y 2 ) with (7x 2 – 5xy – y 2 )
(2x 2 + 3xy + y 2 ) + (7x 2 – 5xy – y 2 ) = (2 + 7) x 2 + (3 – 5) xy + (1 – 1) y 2 = 9x 2 – 2xy
b) Subtract (5ab – 3bc + a 2 ) from (ab + 9bc – a 3 )
It is important to note that the minus sign in front of the parentheses reverses all the signs inside the parentheses.
(5ab – 3bc + a 2 ) – (ab + 9bc – a 3 ) = 5ab – 3bc + a 2 – ab – 9bc + a 3 =
(5 – 1) ab + (- 3 – 9) bc + a 2 + a 3 = 4ab -12bc + a 2 + a 3
Multiplication
Algebraic multiplication is done by multiplying term by term.
To multiply the literal part, we use the potentiation property to multiply the same base: “the base is repeated and the exponents are added”.
Example
Multiply (3x 2 + 4xy) with (2x + 3)
(3x 2 + 4xy). (2x + 3) = 3x 2 . 2x + 3x 2 . 3 + 4xy. 2x + 4xy. 3 = 6x 3 + 9x 2 + 8x 2 y + 12xy
Division of a polynomial by a monomial
Dividing a polynomial by a monomial is done by dividing the coefficients of the polynomial by the coefficient of the monomial. In the literal part, the property of the power division of the same base is used (the base is repeated and subtracts the exponents).
Example
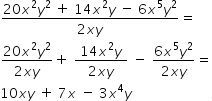
Exercises
1) Being a = 4 and b = – 6, find the numerical value of the following algebraic expressions:
a) 3a + 5b
b) a 2 – b
c) 10ab + 5a 2 – 3b
Answer:
a) 3.4 + 5. (- 6) = 12 – 30 = – 18
b) 4 2 – (-6) = 16 + 6 = 22
c) 10.4. (-6) + 5. (4) 2 – 3. (- 6) = – 240 +80 + 18 = – 240 + 98 = – 142
2) Write an algebraic expression to express the perimeter of the figure below:

P = 4x + 6y
3) Simplify the polynomials:
a) 8xy + 3xyz – 4xyz + 2xy
b) a + b + ab + 5b + 3ab + 9a – 5c
c) x 3 + 10x 2 + 5x – 8x 2 – x 3
Answer:
a) 10xy – xyz
b) 10a + 6b – 5c + 4ab
c) 2x 2 + 5x
4) Being,
A = x – 2y
B = 2x + y
C = y + 3
Calculate:
a) A + B
b) B – C
c) A. Ç
Answer:
a) 3x -y
b) 2x – 3
c) xy + 3x – 2y 2 – 6y
5) What is the result of dividing the polynomial 18x 4 + 24x 3 – 6x 2 + 9x by the 3x monomial?View Answer
6x 3 + 8x 2 – 2x + 3